In the chapter 1.2 of Michael Nielsen’s book Quantum Comutation and Quantum Information, it is said that the state of a qubit could be rewritten as \begin{equation}\label{eq_bloch} |\psi\rangle = \cos\frac{\theta}{2}|0\rangle + e^{i\varphi}\sin\frac{\theta}{2}|1\rangle, \end{equation} but the inference procedure was not given. Here we try to infer it.
Let $z=x+iy$ be a complex number, where $x$ and $y$ are real numbers, and $i$ is the imaginary unit. Let $$ r=\|z\|^2 = x^2 + y^2 $$ be the norm of $z$. Then the complex number $z$ could be considered as a point $Z$ on the circle with the origin $O$ as its center and $r$ as its radius.
Let $\theta$ be the angle between the vector $\vec{OZ}$ and the positive direction of the $x$ axis. The complex $z$ could be represented as $$ z=r(\cos\theta + i\sin\theta). $$
According to the Euler’s formula $e^{i\theta}=\cos\theta + i\sin\theta$, we have \begin{equation}\label{eq_complex} z=re^{i\theta}$. \end{equation}
Suppose the state of a qubit is represented as $|\psi\rangle=\alpha|0\rangle + \beta|1\rangle$, where $\alpha$ and $\beta$ are both complex numbers. According to \eqref{eq_complex}, $\alpha$ and $\beta$ could be rewritten as \begin{align*} \alpha &= r_{\alpha}e^{i\theta_{\alpha}} \\ \beta &= r_{\beta}e^{i\theta_{\beta}}, \end{align*} and therefore $|\psi\rangle$ could be rewritten as \begin{equation}\label{eq_psi} |\psi\rangle=r_{\alpha}e^{i\theta_{\alpha}}|0\rangle + r_{\beta}e^{i\theta_{\beta}}|1\rangle. \end{equation}
Multiply $e^{-i\theta_{\alpha}}$ to the both side of the equation \eqref{eq_psi}, we have \begin{align*} |\psi’\rangle &= e^{-i\theta_{\alpha}} |\psi\rangle \\ &= r_{\alpha}|0\rangle + r_{\beta}e^{i(\theta_{\beta}-\theta_{\alpha})}|1\rangle \\ &= r_{\alpha}|0\rangle + r_{\beta}e^{i\theta}|1\rangle, \end{align*} where $\theta = \theta_{\beta}-\theta_{\alpha}$.
Note that $\|e^{-i\theta_{\alpha}}\|^2 = 1$, it’s easy to see that \begin{align*} |\psi’\rangle &= e^{-i\theta_{\alpha}} |\psi\rangle \\ &= e^{-i\theta_{\alpha}}\alpha |0\rangle + e^{-i\theta_{\alpha}}\beta |1\rangle \end{align*} has the same measurement effect as $|\psi\rangle$, since $|e^{-i\theta_{\alpha}}\alpha|^2 = |\alpha|^2$ and $|e^{-i\theta_{\alpha}}\beta|^2 = |\beta|^2$. Therefore, we could substitute $|\psi\rangle$ with $|\psi’\rangle$.
Finally, since $$ |\psi’\rangle = r_{\alpha}|0\rangle + r_{\beta}e^{i\theta}|1\rangle, $$ and let $r_{\beta}e^{i\theta}=x+iy$, where $x$ and $y$ are both real numbers, then \begin{equation}\label{eq_psi_prim} |\psi’\rangle = r_{\alpha}|0\rangle + (x+iy)|1\rangle. \end{equation}
According to the normalization condition, we have $|r_{\alpha}|^2+|(x+iy)|^2=1$, that is, \begin{align*} |r_{\alpha}|^2 + |(x+iy)|^2 &= r_{\alpha}^2 + (x+iy)(x-iy) \\ &= r_{\alpha}^2 + x^2 + y^2 \\ &= 1, \end{align*} i.e., \begin{equation}\label{eq_coordinate} r_{\alpha}^2 + x^2 + y^2 = 1, \end{equation} 
where $r_{\alpha}$, $x$ and $y$ are both real numbers. The equation \eqref{eq_coordinate} shows that $(x,y,r_{\alpha})$ is the coordinate of a point on the unit sphere of the three dimension space.
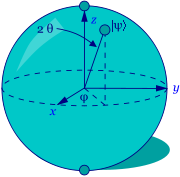
In the polar coordinate system, the point $(x,y,r_{\alpha})$ on the unit sphere could be represented as \begin{align*} x &= r \sin\theta\cos\varphi \\ y &= r \sin\theta\sin\varphi \\ r_{\alpha} &= r\cos\theta \end{align*} where $r=1$ is the radius of the unit sphere.
Therefore, according to \eqref{eq_psi_prim}, the state of a qubit could be rewritten as \begin{align} |\psi’\rangle &= \cos\theta|0\rangle + (\sin\theta\cos\varphi + i\sin\theta\sin\varphi)|1\rangle \notag \\ &= \cos\theta|0\rangle + (\cos\varphi + i\sin\varphi)\sin\theta|1\rangle \notag \\ &= \cos\theta|0\rangle + e^{i\varphi}\sin\theta|1\rangle.\label{eq_psi_polar} \end{align}
But wait, the formula \eqref{eq_psi_polar} slightly differs from the formula \eqref{eq_bloch}. We have to transform the $\theta$ to $\frac{\theta}{2}$.
Suppose \begin{equation}\label{eq_psi_sphere} |\psi\rangle = \cos\theta’|0\rangle + e^{i\varphi}\sin\theta’|1\rangle. \end{equation} Note that if $\theta’=0$ then $|\psi\rangle= |0\rangle$, and if $\theta’=\frac{\pi}{2}$ then $|\psi\rangle=e^{i\phi}|1\rangle$, which shows that if $0\leq\theta’\leq\frac{\pi}{2}$, \eqref{eq_psi_sphere} could represents any point on a Bloch sphere.
Suppose the point corresponding to a qubit state $|\psi’\rangle$ is symmetrical to the point corresponding to a qubit state $|\psi\rangle$, relative to the center of the Bloch sphere. Obviously the polar coordinate of $|\psi’\rangle$ is $(1, \pi-\theta’, \varphi+\pi)$, i.e., \begin{align*} |\psi’\rangle &= \cos(\pi-\theta’)|0\rangle + e^{i(\varphi+\pi)}\sin(\pi-\theta’)|1\rangle\\ &= -\cos\theta’|0\rangle + e^{i\varphi}e^{i\pi}\sin\theta’|1\rangle\\ &= -\cos\theta’|0\rangle - e^{i\varphi}\sin\theta’|1\rangle\\ &= - |\psi\rangle, \end{align*} which means the point corresponding to $|\psi’\rangle$ on the lower half sphere differs from its symmetry point corresponding to $|\psi\rangle$ on the upper half sphere with a phase of $-1$. Therefore we could consider only the points on the upper half sphere correponding to a $\theta’$ satisfying $0\leq\theta’\leq\frac{\pi}{2}$.
Finally we will map the points on the upper half sphere to the points on the whole sphere. Let $\theta=2\theta’$, i.e., $\theta’=\frac{\theta}{2}$, then we have \begin{equation}\label{eq_finally} |\psi\rangle = \cos\frac{\theta}{2}|0\rangle + e^{i\varphi}\sin\frac{\theta}{2}|1\rangle, \end{equation} where $0\leq\theta\leq\pi$ and $0\leq\varphi\leq 2\pi$ is the polar coordinate of the corresponding point on the Bloch sphere. Note that the equation \eqref{eq_finally} is exactly the same as the equation \eqref{eq_bloch}.
